Sysquake Pro – Table of Contents

Sysquake – Table of Contents

Sysquake for LaTeX – Table of Contents

convolution.sq

Convolution and correlation of signals

SQ file convolution.sq illustrates how convolution and correlation products are calculated.

First contact

The convolution product of two signals x(t) and y(t), denoted x(t)*y(t), is defined as

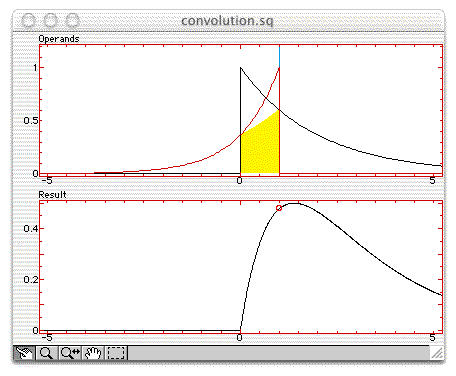
When convolution.sq is opened, the convolution product of two exponential signals is performed. The upper figure shows the integral for a given value of t, represented as a red circle in the result displayed in the lower figure. The integral, shown as a yellow region, is the product of x and a flipped y shifted by t. You can change t with the mouse either by sliding the whole flipped y in the upper figure, or by moving the red circle on the result. You can change the signals in the Settings menu.

Settings

In the Settings menu, you can switch among several pairs of signals. You can also display the correlation of an exponential with itself (autocorrelation), or the correlation between a square corrupted by noise with a square (signal detection). The correlation is similar to the convolution product; the differences are that no signal is flipped, and the result is a function of the shift tau instead of the time t:

Squares

Convolution between two squares of the same length.

Exponentials

Convolution between two exponential signals with different time constants.

Delayed Exponential

Convolution between an exponential and a delayed Dirac impulsion, which yields a delayed exponential.

Echo

Convolution between an exponential and two Dirac impulsion, which yields an exponential with an echo.

Step Response

Convolution between a step and an exponential; if the exponential is the impulse response of some first-order system and the step is its input, their convolution product is the system output (the step response of the first-order system).

Autocorrelation of Exponentials

Autocorrelation of an exponential, which yields a symmetric function with a maximum at 0.

Signal Detection

Cross-correlation between a square signal corrupted by noise and a pure square. Despite the high level of noise, the result shows a clear maximum which indicates when the square occurs.

Figures

First/Second Operand

The operands of the convolution product or the arguments of the correlation product are displayed. They cannot be manipulated.

Operands

The operands of the convolution or the arguments of the correlation are displayed. For the convolution, the second operand is displayed backward and can be shifted by a value of tau. For the correlation, the second argument is shifted by a value of t. In both cases, the product of both signals is displayed as a yellow area, whose surface (integral) represents the value of the result for the specified shift. The shift can be manipulated interactively.

Result

The result (convolution or correlation) is displayed in black, with a red circle to highlight the value corresponding to the shift represented in the Operands figure. This circle can be dragged interactively.