RST_dt.sq

Discrete-time two-degrees-of-freedom linear controller

RST_dt.sq implements the basic tools for the design of classical controllers for linear SISO discrete-time systems. As a useful extension to design more robust controllers, the system can be modeled by several transfer functions. Even if only one nominal model is used, a very robust controller may be easily obtained with pole placement if the sensitivity functions are taken into account during the design.

The user can provide either a continuous-time model or a discrete-time model. In the second case, the discrete-time model is used as is; the sampling period is used only to scale the times and the frequencies on the display. In the first case, the continuous-time model is sampled with a zero-order hold at the sampling frequency. The continuous-time model is used for the hybrid time responses "Continuous-Time Step Resp. Y/R" and "Continuous-Time Step Resp. Y/D", which better reflects the reality, especially when the sampling period is large with respect to the system; the curve displayed represents the output of the continuous-time system when the controller is digital and interfaced with the system through a zero-order hold and a sampler.

First contact

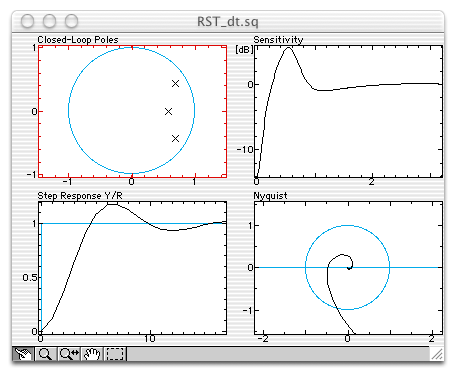
When you open RST_dt.sq from Sysquake (menu File/Open), four figures are displayed: the closed-loop poles, the Bode magnitude, the step response, and the Nyquist diagram. They correspond to a first-order system and a second-order controller with a scalar feedforward calculated to remove steady-state error. You can move the closed-loop poles by dragging them with the mouse. You can also change the gain of the feedback by dragging the Bode magnitude up and down. Observe what happens when you drag the poles outside the unit circle: the closed-loop system becomes unstable, the step response becomes very large, and the Nyquist diagram crosses the critical point -1.

How to use it

Many standard graphics are implemented. Among the possible designs, the easiest to use is pole placement, where the closed-loop poles are moved into the desired region inside the unit circle, the stability region which plays the same role for discrete-time systems as the left half-plane for continuous-time systems. Caution must be exercised about the robustness of the controller, because pole placement itself can lead to extremely unrobust designs. Fortunately, by observing simultaneously robustness indicators such as the sensitivity function, the Nyquist diagram or robustness margins, it is easy to avoid this pitfall.

Figures

Step Response Y/U

Open-loop step response, useful to get an idea of the dynamics of the system.

Impulse Response Y/U

Open-loop impulse response. Depending on the system and the preferences of the user, the impulse response may be better to represent the dynamics of the system. The presence of an integrator, for instance, may make the step response more difficult to understand.

Step Response Y/R

Tracking closed-loop step response. This step response shows important transient effects of the controlled system, such as the overshoot, the rise time, the settling time. The tracking steady-state error (or lack of it) is also visible. The input/output stability is usually immediately visible, unless a very slow unstable mode is hidden by the limited range of time. Beware of potential internal unstable modes.

Step Response U/R

Tracking closed-loop step response between the reference signal and the system input. Risks of saturation, high-frequency modes (ringing), and slow or unstable internal modes are clearly visible and complete the time-domain information obtained with the step response of Y/R.

Step Response Y/D

Disturbance rejection step response. The disturbance step is applied to the output of the system. This response may be very different from the tracking step response, especially with two-degrees-of-freedom controllers where the prefilter polynomial T(z) is tuned to cancel closed-loop poles or to make the tracking faster.

Step Response U/D

Step response between a disturbance and the system input.

Ramp Response Y/R

Tracking closed-loop ramp response. This response may be better suited to the study of transient effects and permanent error than the step response if the real set-point changes with a fixed rate.

Ramp Response Y/D

Tracking closed-loop ramp response between a disturbance and the system output.

Continuous-Time Step Response Y/R and Y/D

If a continuous-time model of the system is provided, what happens between the samples can be displayed by the continuous-time step responses. The continuous-time system input is obtained by converting the discrete-time samples with zero-order hold. The discrete-time step responses representing the output is displayed with straight lines joining each samples. This approximates correctly the continuous-time responses if the sampling period is small enough with respect to the dynamics of the open-loop system. Otherwise, the continuous-time responses should be used.

Bode Magnitude and Phase

Open-loop frequency response, displayed as functions of the frequency expressed in radians per time unit. The cross-over slope of the magnitude, and the low- and high-frequency open-loop gains give important insights about the robustness of the controller.

The Bode magnitude can be dragged up and down to change the gain of the controller.

Nyquist

Open-loop frequency response, displayed in the complex plane. The phase is expressed in radians. The gain and phase margins are clearly visible. With high-order systems and controllers, make sure that the system is stable by inspecting the closed-loop poles, the robustness margins (where the stability is explicitly checked) or at least a time-domain response.

Nichols

Logarithm of the frequency response, displayed in the complex plane. The phase is expressed in radians. The gain and phase margins are clearly visible.

The Nichols diagram can be dragged up and down to change the gain of the controller.

Sensitivity

Closed-loop frequency response between an output disturbance and the output. Only the amplitude is displayed, which is enough to give important information about the robustness of the design. Its supremum is the inverse of the modulus margin, which is defined as the distance between the Nyquist diagram and the critical point -1 in the complex plane. Peaks and large values of the sensitivity should be avoided. The sensitivity should be small at low frequency, to make the behavior of the system insensitive with respect to model uncertainties in the bandwidth.

Complementary Sensitivity

Closed-loop frequency response between measurement noise and the output. Its name comes from the fact that the sum of the sensitivity and the complementary sensitivity is 1 for any frequency (however, this does not apply to their amplitude). In the case of a one-degree-of-freedom controller, the complementary sensitivity is also the frequency response between the set-point and the output. It should be close to 1 at low frequency, and small at high frequency.

Perturbation-Input Sensitivity

Closed-loop frequency response between output disturbance and the system input. Small values at high frequency reduce the excitation of the actuators in presence of measurement noise.

Open-Loop Zeros/Poles

All the open-loop zeros and poles are represented. The zeros and poles of the system are represented by black circles and crosses, respectively. The zeros and poles of the free part of the feedback are represented by red circles and crosses; the zeros and poles of the fixed part of the feedback are represented by green circles and crosses; the fixed part of the feedforward polynomial is represented by green squares. All the zeros and poles of the controller can be manipulated with the mouse. The system cannot be changed. As an help to cancel some of the dynamic of the closed-loop system with the feedforward zeros, the closed-loop poles are displayed as magenta (pink) dots.

Closed-Loop Poles

The closed-loop poles are displayed as black crosses. If there are as many closed-loop poles as free coefficients in the feedback, they can be moved; a new controller is calculated by pole placement.

Root Locus

The root locus is the locus of the closed-loop poles when the gain of the feedback is a positive real number. The zeros and poles of the feedback are preserved. The open-loop zeros and poles are represented by black circles and crosses for the system, and red circles and crosses for the feedback. Feedback zeros and poles can be dragged to change the controller. The closed-loop poles are represented by triangles. They can be moved on the root locus to change the feedback gain. If they move beyond open-loop zeros and poles, the sign of the feedback changes, and the root locus is inverted.

Robustness Margins

The gain margin (in dB) and phase margin (in degrees) are displayed with the corresponding frequencies (in radians per time unit). For unstable open-loop systems, the gain margin can be negative and is a lower stability limit for the feedback gain. If the closed-loop system is unstable, no margin is displayed. If the open-loop gain is smaller or larger than 1 at all frequencies, the phase margin is not displayed.

Settings

System (Continuous-Time Model)

A continuous-time model can be given as two row vectors which contain the numerator and denominator of a transfer function. Multiple models can be provided; each model corresponds to a row. The continuous-time model is converted to a discrete-time model sampled at the sampling period given in the setting Sampling Period using a zero-order hold. The continuous-time model is used only by the continuous-time step responses; all the other figures are based on the discrete-time models.

System (Discrete-Time Model)

A discrete-time model is given as two row vectors which contain the numerator and denominator of a transfer function. Multiple models can be provided; each model corresponds to a row. If a discrete-time model is provided, the continuous-time model is ignored and the continuous-time step responses cannot be displayed.

Sampling Period

The sampling period is given as a positive pure number. It is used for the scale of time- and frequency-domain responses. The unit is implicit and could be seconds or anything else (minutes, hours, days, etc.)

Feedback Coefficients

The coefficients of the numerator and denominator of the feedback are given as two row vectors. If they are not factors of the feedback fixed parts (see below), the user is asked whether he wants to modify them.

Feedback Fixed Parts

The coefficients of the fixed parts of the numerator and denominator of the feedback are given as two row vectors. The fixed parts can be used to impose some poles and zeros in the feedback (for instance an integrator with [1,-1] in the denominator); they are enforced during pole placement. The gain is meaningless; only the zeros are used. When the fixed parts are changed, a new controller is computed such that the closed-loop poles are preserved. If this is not possible because there are not enough closed-loop poles to permit pole placement, the variable part of the controller is preserved. If the resulting controller (product of fixed and variable parts) is non-causal, it is delayed with additional poles at 0.

Two DOFs

The Two DOFs setting is a binary value which enables an arbitrary feedforward polynomial. Otherwise, the feedforward is set to the same value as the feedback numerator; this means that the error between the system output and the set-point is used as a whole to compute the system input. When Two DOFs is enabled, the feedforward contains the zeros of its fixed part (see below), and its gain is calculated to have a unit gain between the set-point and the system output.

Feedforward Fixed Part

The feedforward fixed part is given as a row vector. It provides all the zeros of the feedforward; its gain is ignored. The Feedforward Fixed Part setting is enabled only for two-degrees-of-freedom controllers.

Characteristic Polynomial

The controller can be calculated by specifying directly the characteristic polynomial, i.e. the denominator of all the closed-loop transfer functions which can be defined, whose roots are the closed-loop poles. To enter the closed-loop poles, use the poly function (e.g. poly([0.8,0.6+0.3j,0.6-0.3j])).

In order to obtain a solution for any value of the coefficients, the degree of the characteristic polynomial must be larger than or equal to 2 deg A + deg Rf + deg Sf - 1, where A, Rf and Sf are respectively the system denominator, the fixed part of the feedback denominator and the fixed part of the numerator. This lower limit is displayed in the dialog box. There is no upper limit (from a mathematical point of view).

Damping Specifications

Absolute and relative damping can be specified; they are represented in the complex plane of the closed-loop poles and the root locus by red lines. For a stable system, the absolute damping is the absolute value of the slowest pole; the relative damping is the absolute damping divided by the oscillation time expressed in sampling periods.

Display Frequency Line

When selected, moving the mouse above a frequency response (Bode or sensitivity) will display a corresponding line in other frequency responses, Nyquist diagrams, and zero/pole diagrams.