Sysquake Pro – Table of Contents
Sysquake for LaTeX – Table of Contents
GPC.sq
Design of a linear Generalized Predictive Controller
A GPC (Generalized Predictive Controller) is a controller which minimizes
the error between the desired future set-point and the predicted system output.
The predicted output is based on a model of the system, the past input (control
signal) and output (measures), and the future control signal. Minimizing the
future error leads to the "best" sequence of future control signal
samples. Only the first sample is actually used; other ones are discarded,
and a new optimization is performed for the next sample, to take into account
as well as possible the past disturbances though their effect on the measured
output. With the GPC, the system input is supposed to be constant after some
time, called the control horizon
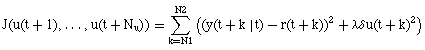
where
First contact
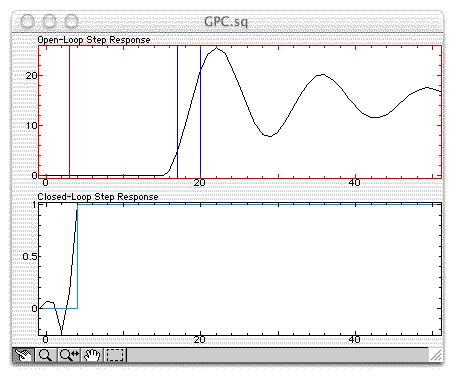
When you open GPC.sq from Sysquake (menu File/Open), two figures are
displayed
Figures
Open-Loop Step Response
The open-loop step response of the system is displayed in black. The control horizon is displayed as a red vertical line, and the prediction horizon as two blue vertical lines. For best results, the range delimited by the prediction horizon should include at least the first oscillation of the system step response. The horizons can be manipulated.
Closed-Loop Step Response
The closed-loop step response of the controlled system is displayed in black, and the set-point (step) is displayed in light blue.
Closed-Loop Input Response
The input (control signal) of the closed-loop step response of the controlled system is displayed in black.
Closed-Loop Poles
The closed-loop poles are displayed as crosses in the complex plane, and the closed-loop zeros are displayed as circles. Note that for high-order systems, such as those with large delays, the numeric computation of roots may give inaccurate or totally wrong results.
Settings
System
The transfer function of the system can be given in a dialog box as two polynomials, highest power first. Systems with delays have poles at 0, i.e. trailing zeros in the list of denominator coefficients.
Input Weight
The input weight